Creating word search boards

If an alien threatened to harm my goldfish unless I told it how to programatically generate a word search game/board, how would I do it? Alright, it's not that serious and no goldfishes were harmed in entertaining this prompt.

For posterity, this is word search.

I deployed a word search generator to JAM Arcade recently and wanted to share how it manifested. You know, it would have been great to say this was a breeze and a walk in a park to figure out, especially efficiently, but it was a struggle, or euphemistically, a journey.

Let's start with context. The idea of creating a word search generator probably came about 2016 - 2017. I started scribbling brief notes and exploring different methods to generate an N x N or N x M board programmatically, but arugably spent way more time thinking about performance. I'll add color to this in a follow-up, but how do I know what word or words could fit where at a given time on the board?

The onion analogy is overused, but might be a decent one to use in this case. Envision a finished board and step or work backwards to identify the layers. We'd probably conclude by evaluating potential approaches that could generate these boards programmatically. To digress a bit, it's worth noting board generation from a predetermined list of words is a much different beast than generating a board from non-predermined list of words. We'll focus the discussion on the latter.

So working backwards, what do we have? If the finished board is made up of searchable words, the other letters filling up the rest of the board or non-words, are probably randomly selected letters. Given that, outside of p number of words selected for a given completed game board, which words get chosen, how do they get chosen and where do the words come from?

We should have a mental model of how this might work conceptually. Let's walk through it and perhaps discuss some pitfalls along the way as well.

First off, we need a dictionary of words available to us. On a Mac, your machine should come with a Dictionary.app application. That's a good place to start, otherwise, there are other sources could potentially be leveraged.

With a dictionary in hand, let us consider how to put words onto a board until each cell in the grid is filled with a letter. Like many things in life, we can make progress by building on top of previous steps; or in this case, one word at a time. As each potential word fill up the grid, there should be a terminal condition to prevent further words from being inserted onto the grid right? Afterall, the grid fills up and it's not a great experience if you even manage to fill up every empty cell on a board with a word. If that sounds like a plan, let's get into the nitty gritty.

Assume English and an N x N or N x M board and we'll discover rules and conditions as we walk through what should be considered.

• The maximum length of a word is the upper bound of a given board's size. In n x n, it would be n and in an n x m board, it would depend on whether n or m is larger. This makes sense because you can't have a valid word that is longer than the length of the chosen board.

MAX_WORD_LEN = max(board_length)

• The minimum length of a word is subjective. You could have one character letters as words such as "a", or perhaps two character words such as "to" or "in", but I'd argue the cons outweigh the pros of setting a minimum word length of 2 or less. Instead, I'd opt for a minimum word length of at least 3.

# Three is pretty good. Average word length is ~4.7 characters (round upto 5)
MIN_WORD_LEN = 3

• Next is the sense of "direction". There isn't a "correct" direction a word must be placed in a word search grid so long as a word is placed in a straight line starting at either a cardinal direction or ordinal direction and it's corresponding opposite direction. That may have been too verbose. In other words, a word should either be placed NS or SN, WE or EW, NESW or SWNE, NWSE or SENW within the word search grid.

# Direction doesn't have to be an enum, but we'll use it in this example
from enum import Enum
from random import choice

class Direction(Enum):
  NS = 0
  WE = 1
  NWSE = 2
  SWNE = 3
  SN = 4
  EW = 5
  SENW = 6
  NESW = 7

selected_direction = choice(list(Direction))

Is that it? Do we have enough information now to put a word search game together with these three rules? We could. It would probably be uninteresting though. As we start picking random spots to inject words into the grid, we'll find out pretty quickly that the first word and direction chosen to place within the grid will influence the rest of the board; namely it'll just be a bunch of words that fit into the grid in the same direction. Why? Because we haven't accounted for finding words that might share one or more characters with existing words on the board. We haven't told our program how to handle a scenario like this. We need to give words selected the ability to intersect with any of the 8 directions should they share a letter in any given cell.

Then there must be another constraint!

• For a given direction to insert a word with a known word length of being between the maxium length and minimum length, which cells will have shared characters and what position are those characters in?

Here's an example: Let's say COY and CHEESE are words that have been populated on the board previously. A few cycles later, pseudorandomization decides it wants a 4 letter word that either begins with YC or ends with CY. In a dictionary, we know that pacy, lacy or racy would be valid words to insert based on those consraints.

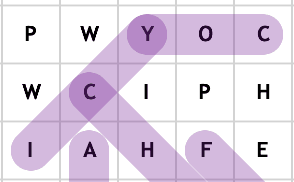
Let's look back really quick. Is that enough for us to go by to generate a board? For the most part, yes. You could have a recursive or iterative method call to populate the board by looking for a set of words to select from given the constraints of any given open cell in the grid. If there are no words that fit that criteria, that's okay - we just don't insert a word at the interation and find another open cell with another set of constraints. Then at what point do you terminate the call? It's usually reasonable to terminate when you have say 30% +/- a few percentage points of a board filled with words to find. The rest of the cells should be populated by random letters.

Here's a very rough and bloated example of what that code might look like:

# Return a set or a collection of words to randomly select
class WordSearchBoard:
	# ...

	def find_valid_words(self):
		open_grid_idx = random.choice(self.open_board)
		# Note: You may want to bias word len for various reasons
		# If so, see: https://stackoverflow.com/questions/20311223/how-to-implement-biased-random-function
		word_len = random.randrange(MIN_WORD_LEN, MAX_WORD_LEN)
		dir_dic = find_directions()
		shared_letter_constraints = self.get_letter_constraints(selected_open_grid_idx, word_len, dir_dic)

		# aggregate set / list of words together based on above criteria
		# ...
		word_lists = [[], [], []]
		words_from_constraints = set(word_lists[0]).intersection(*word_lists[1:])

		if len(words_from_constraints) = 0:
			return self.find_valid_words()
		else:
			return { cell_idx: open_grid_idx, words_avail: words_from_constraints }

With that, let's call it for this part. Look out for part II which is equally important if not more important. In the find_valid_words method there's some hand-waving going on with how to get a list of words to select from to place on a board.

Stay tuned!